Quantum Computing Breakthrough Achieves Optimal State Distillation

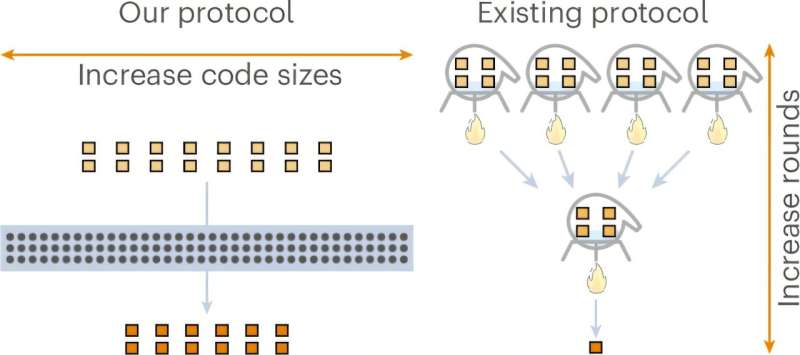
Researchers have achieved a significant milestone in quantum computing by demonstrating that the theoretically optimal scaling for magic state distillation is attainable for qubits. This breakthrough addresses a crucial bottleneck in the development of fault-tolerant quantum systems and marks an improvement on previous results by reaching a scaling exponent of exactly zero. The findings, published in Nature Physics, resolve a longstanding challenge in the field.

Lead author Adam Wills, a Ph.D. student at MIT‘s Center for Theoretical Physics, emphasized the ambitious nature of building quantum computers. “Most of the reason we don’t have quantum computers already is the issue of noise,” Wills noted. Qubits, the building blocks of quantum computing, are highly sensitive and require protection through error-correcting codes. However, these codes typically support only certain operations known as Clifford gates, which alone do not offer a quantum advantage.

To achieve universal quantum computation, researchers must implement non-Clifford operations in a fault-tolerant manner. This is where magic state distillation comes into play. Originally introduced by Bravyi and Kitaev in 2005, this process allows for the generation of special quantum states required to perform essential operations. Despite its potential, magic state distillation has historically been resource-intensive, with the overhead—meaning the number of noisy input states needed to produce a single high-quality output state—increasing as error rates decrease.

The Role of Magic States in Quantum Computing

Magic states serve as a critical resource in quantum computing, enabling operations that extend beyond the capabilities of Clifford gates. These operations are essential for leveraging the unique advantages of quantum systems over classical ones. For instance, a T gate, crucial for universal quantum computation, can be executed by consuming one magic state along with Clifford operations and measurements. Currently, researchers can generate noisy magic states with error rates around 10^-3, but to achieve quantum advantage, these rates need to fall to approximately 10^-7, and for large-scale applications, as low as 10^-15.

Wills and his team focused on optimizing the efficiency of magic state distillation, quantified by its overhead ratio. Over decades, this overhead has been characterized by a scaling exponent denoted as γ (gamma). A lower γ indicates a more efficient distillation process. Previous efforts had achieved γ values, such as 0.678 in 2017 and an approach nearing γ = 0 in 2018, but these required impractically large quantum systems. Wills and his colleagues proved that achieving γ = 0 is feasible, indicating constant overhead regardless of the required purity of the final states.

Innovative Approaches to Overcome Challenges

Wills described the discovery process as unfolding in two significant stages. The initial realization involved recognizing the potential of algebraic geometry codes, which offer robust error correction while accommodating fixed-size quantum systems. This innovation allowed for achieving constant overhead with 1024-dimensional qudits rather than the two-level qubits typically used in practical quantum computing.

The second breakthrough came from insights gained from a textbook authored by Dan Gottesman. By exploring an obscure chapter, the team discovered a method to represent their qudits as sets of qubits. This transformation enabled the conversion of the constant-overhead protocol from qudits to qubits, resulting in 10-qubit magic states that retained high efficiency with minimal overhead loss.

Despite the theoretical nature of these findings, Wills cautions about the gap that remains between theory and practical application. While achieving γ = 0 establishes a fundamental theoretical limit for magic state distillation overhead, the resource requirements for implementation may exceed what current quantum computers can deliver.

Establishing strong theoretical foundations is essential for advancing fault-tolerant quantum computing. “Developing a solid theory of quantum magic is incredibly important for pushing fault-tolerance further in all regimes,” Wills stated. The team is already exploring future directions, including optimizing constant factors and investigating quantum Low-Density Parity-Check (LDPC) code variants.

The implications of this work are significant for the future of quantum computing, paving the way for innovations that may eventually lead to the practical realization of powerful quantum systems.

For more on advancements in technology and science, readers can follow updates from trusted sources like Phys.org and consider contributing to independent science journalism, which plays a vital role in disseminating important research findings.